Cours de seconde sur les fonctions affines
(Dom)
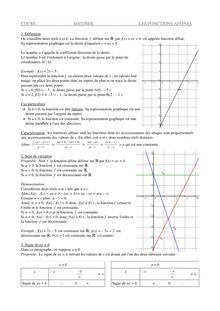
COURS SECONDE LES FONCTIONS AFFINES 1. Définition On considère deux réels a et b. La fonction f définie sur par f(x) = ax + b est appelée fonction affine. Sa représentation graphique est la droite d'équation y = ax + b. Le nombre a s'appelle le coefficient directeur de la droite. Le nombre b est l'ordonnée à l'origine : la droite passe par le point de coordonnées (0 ; b). Exemple : f(x) = 2x – 5 . Pour représenter la fonction f, on choisit deux valeurs de x , on calcule leur image, on place les deux points dans un repère du plan et on trace la droite passant par ces deux points. Si x = 0, f(0) = – 5 ; la droite passe par le point A(0 ; – 5 ). Si x = 2, f(2) = 4 – 5 = – 1 ; la droite passe par le point B(2 ; – 1 ). Cas particuliers : Si b = 0, la fonction est dite linéaire. Sa représentation graphique est une droite passant par l'origine du repère. Si a = 0, la fonction est constante. Sa représentation graphique est une droite parallèle à l'axe des abscisses. Caractérisation : les fonctions affines sont les fonctions dont les accroissements des images sont proportionnels aux accroissements des valeurs de x. En effet, soit u et v deux nombres réels distincts. f u f v au b av b au av a u v Alors = = = = a qui est une constante. u v u v u v u v 2. Sens de variation Propriété : Soit f la fonction affine définie sur par f(x) = ax + b.